求由平面y=0,y=(√3)x,z=0以及球面x^2+y^2+z^2=9 所围成的立体体积

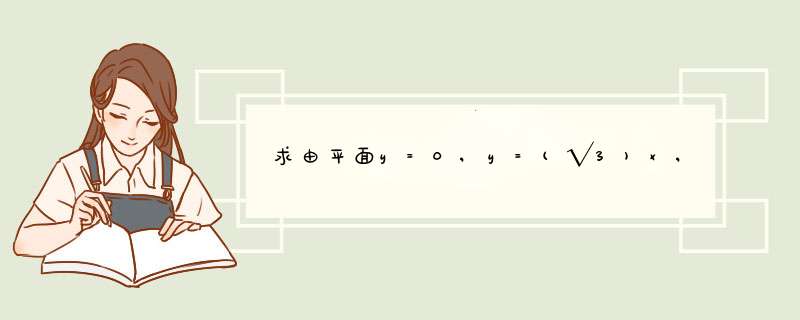
所围成的立体体积V＝(arctank )R^3/3，解答如下:

它是由XOY平面、XOZ平面、垂直于XOY平面的平面y=kx和在第一卦限的球面z=√（R^2-x^2-y^2）所围成的立体图形，在XOY平面的投影是一个扇形，转变成极坐标为：θ=0。θ=arctank，r=R。

V=∫［0，arctank］dθ∫［0，R］√（R^2-r^2）rdr

=-（1/2）∫［0，arctank］dθ∫［0，R］√（R^2-r^2）d（R^2-r^2）

=-（1/2）∫［0，arctank］dθ（R^2-r^2）^（3/2）/（3/2）［0，R］

=（-1/3）∫［0，arctank］（-R^3）dθ

=（R^3/3）θ［0，arctank）

=（arctank）R^3/3

直角坐标系法

适用于被积区域Ω不含圆形的区域，且要注意积分表达式的转换和积分上下限的表示方法：

（1）先一后二法投影法，先计算竖直方向上的一竖条积分，再计算底面的积分。

①区域条件：对积分区域Ω无限制。

②函数条件：对f（x,y,z）无限制。

（2）先二后一法（截面法）：先计算底面积分，再计算竖直方向上的积分。

①区域条件：积分区域Ω为平面或其它曲面（不包括圆柱面、圆锥面、球面）所围成。

②函数条件：f（x，y）仅为一个变量的函数。

http://wlkczzulieducn/kejianweb/gaoshu/9/5ppt

这里有一个幻灯片

其实，三重积分，就是把一重积分和二重积分的扩展

三重积分及其计算

一,三重积分的概念

将二重积分定义中的积分区域推广到空间区域,被积函数推广到三元函数,就得到三重积分的定义

其中 dv 称为体积元,其它术语与二重积分相同

若极限存在,则称函数可积

若函数在闭区域上连续, 则一定可积

由定义可知

三重积分与二重积分有着完全相同的性质

三重积分的物理背景

以 f ( x, y, z ) 为体密度的空间物体的质量

下面我们就借助于三重积分的物理背景来讨论其计算方法

二,在直角坐标系中的计算法

如果我们用三族平面 x =常数,y =常数, z =常数对空间区域进行分割那末每个规则小区域都是长方体

其体积为

故在直角坐标系下的面积元为

三重积分可写成

和二重积分类似,三重积分可化成三次积分进行计算

具体可分为先单后重和先重后单

①先单后重

——也称为先一后二,切条法( 先z次y后x )

注意

用完全类似的方法可把三重积分化成其它次序下的三次积分

化三次积分的步骤

⑴投影,得平面区域

⑵穿越法定限,穿入点—下限,穿出点—上限

对于二重积分,我们已经介绍过化为累次积分的方法

例1 将

化成三次积分

其中 为长方体,各边界面平行于坐标面

解

将 投影到xoy面得D,它是一个矩形

在D内任意固定一点(x ,y)作平行于 z 轴的直线

交边界曲面于两点,其竖坐标为 l 和 m (l < m)

o

x

y

z

m

l

a

b

c

d

D

(x,y)

例2 计算

其中 是三个坐标面与平面 x + y + z =1 所围成的区域

D

x

y

z

o

解

画出区域D

解

除了上面介绍的先单后重法外,利用先重后单法或切片法也可将三重积分化成三次积分

先重后单,就是先求关于某两个变量的二重积分再求关于另一个变量的定积分

若 f(x,y,z) 在 上连续

介于两平行平面 z = c1 , z = c2 (c1 < c2 ) 之间

用任一平行且介于此两平面的平面去截 得区域

则

②先重后单

易见,若被积函数与 x , y 无关,或二重积分容易计算时,用截面法较为方便,

就是截面的面积,如截面为圆,椭圆,三角形,正方形等,面积较易计算

尤其当 f ( x , y , z ) 与 x , y 无关时

 首先求内力的方法是截面法，即用假想的截面将所要求的截面截成两段，取其中一段作为研究对象，该部分上所作用的外荷载与所截开的截面上的内力构成平衡力系，利用平衡方程即可求出该截面上的内力了。

若求杆件上各的内力，用截面法逐次求各截面就行了。

轴力图的画法与上面方法类似，就是先求出控制面上的轴力，然后将相邻两控制面上的轴力值连成线，即完成了轴力图。

控制面包括：集中荷载的两侧，分布荷载的起点和终点。