△ABC中，以AB，AC为边向外作正方形ABGF和正方形ACDE，PQ过A且垂直BC于P。求证；FQ=EQ

给你一个提示吧，相信你看完提示就会了

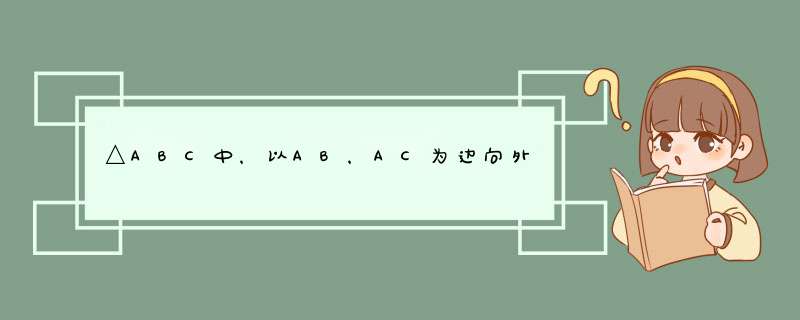
过E做PQ延长线的垂线，垂足为M

过F做PQ的垂线，垂足为N

容易证明：△CPA全等于△AME得到：AP=EM

△BPA全等于△ANF得到：AP=FN

于是EM=FN

再证明：△FNQ全等于△EMQ（AAS）

得到：FQ=EQ

相信你其中三个全等你能找到条件证明吧

∵AB‖CD,

∴∠AEN=∠CFE,

∵∠AEP=∠CFQ

∴∠AEN – ∠AEP=∠CFE-∠CFQ

即∠PEN=∠QFE

∴PE‖QF

∴∠EPM=∠FQM