ABCD-EFGH是一个正方体，其中棱长AB=a。试求

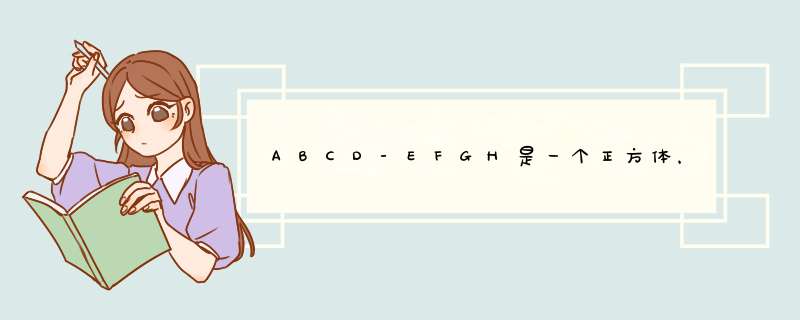
(1)可以根据面积射影定理来求

连接BG,由正方体的性质可知,H在面BCGF的射影是G,A在面BCGF的射影是B

∴△BCG是△ACH在面BCGF的射影

AC=AH=CH=√2a,S△ACH=√3/4(√2a)²=√3/2a²

S△BCG=1/2a²,∴cosθ=S△BCG/S△ACH=1/√3

θ=arccos(√3/3)

(2)连接FA,FC,FH,则FA=FC=FH=√2a

∴F在面ACH的射影O是△ACH的外心

OH=AH/√3=√2/√3a

勾股定理得OF=2√3/3a

哈夫曼树为：

1 |-----042 |-----019 |-----008 |-----003

|-----005

|-----011

|-----023

|-----058 |-----029

|-----029 |-----014

|-----015 |-----007

|-----008

这八个字符的编码分别为：（005）的编码0001，（029）的编码10, （007）1110， （008）1111，（014）110，（023）01，（003）0000，（011）001

设CB、FG交点为M

FM=200-4=196

因为四边形ABCD与四边形EFGH是两个相同的直角梯形

同时减去四边形ABMF得到：

一号区的面积

=梯形FPCM的面积

=（196+200）21/2

=396

b———ah———g

c————de————f

连接ac，在菱形ABCD中，对角线垂直，即ac⊥bd(be),记ac和be的交点为w,则△baw为直角三角形

直角为角bwa

因为两个菱形完全一样，则∠bac和∠hge相等

在△baw 和△bge中：

∠baw=∠hge

∠wba = ∠ebg(公共角)

所以∠bwa=∠beg=90°

所以三角形beg一定是一个直角三角形

（1）因为棱AB在平面ABCD和平面ABFE中，所以与棱AB异面的棱有：棱EH、棱FG、棱DH、棱CG、棱GH．

（2）因为棱AB在平面ABCD和平面ABFE中，所以与它平行的平面是平面EFGH和平面CDHG．

（3）因为平面ABCD是长方体的下面，所以与它垂直的平面是长方体的前、后、左、右4个侧面，即平面ABFE、平面BCGF、平面CDHG、平面ADHE．

故答案为：（1）棱EH、棱FG、棱DH、棱CG、棱GH；（2）平面EFGH和平面CDHG；（3）平面ABFE、平面BCGF、平面CDHG、平面ADHE．