根号三是无理数吗

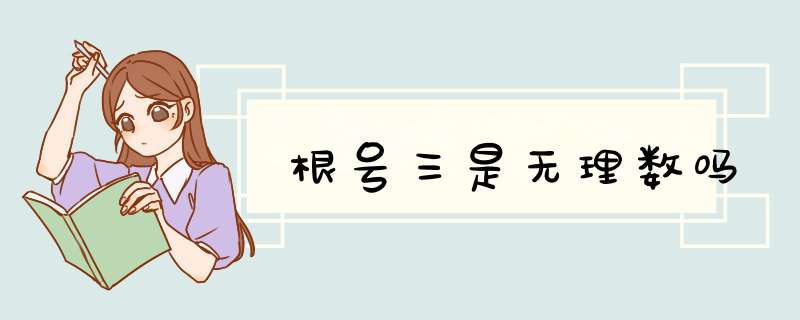
根号3是一个无理数。

因为它的小数部分是无限不循环的，无论算多久也算不出小数部分的规律。无理数，也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环。常见的无理数有非完全平方数的平方根、π和e（其中后两者均为超越数）等。

扩展资料：

在数学中，无理数是所有不是有理数字的实数，后者是由整数的比率（或分数）构成的数字。当两个线段的长度比是无理数时，线段也被描述为不可比较的，这意味着它们不能“测量”，即没有长度。常见的无理数有：圆周长与其直径的比值，欧拉数e，黄金比例φ等等。

无理数也可以通过非终止的连续分数来处理。无理数是指实数范围内不能表示成两个整数之比的数。简单的说，无理数就是10进制下的无限不循环小数，如圆周率。而有理数由所有分数，整数组成，总能写成整数、有限小数或无限循环小数，并且总能写成两整数之比，如21/7等。

希伯索斯的发现，第一次向人们揭示了有理数系的缺陷，证明了它不能同连续的无限直线等同看待，有理数并没有布满数轴上的点，在数轴上存在着不能用有理数表示的“孔隙”。而这种孔隙经后人证明简直多得“不可胜数”。

于是，古希腊人把有理数视为连续衔接的那种算术连续统的设想彻底地破灭了。不可公度量的发现连同芝诺悖论一同被称为数学史上的第一次数学危机。

对以后2000多年数学的发展产生了深远的影响，促使人们从依靠直觉、经验而转向依靠证明，推动了公理几何学和逻辑学的发展，并且孕育了微积分思想萌芽。

根号三是一个非常特殊的数值，它可以用简单的计算方式得出。首先，我们需要知道什么是平方根。平方根其实就是一个数的平方等于给定的值，例如4的平方根就是2，因为2 x 2 = 4。同样地，根号三就是我们需要找一个数，这个数和它本身相乘等于三。这个数是没有办法用有限的小数表示出来的，因为三不是一个完全平方数。但是我们可以使用无限循环的小数来接近这个数值。

为了计算根号三，我们可以使用一个叫做长除法的方法。我们需要确定一个初始值，这个初始值和它本身相乘等于三。一个很好的初始值是15。从这里开始，我们需要进行下列步骤：首先，将3除以15。这个值的商是2。将商和被除数相加，然后除以2。这个结果是175。接着，再用3除以175，商是17142857。将这个数和175相加，然后除以2。这个结果是17321428。这个数字非常接近根号三了。

当我们进行长除法来计算根号三的时候，我们会发现一个有趣的现象。我们可以不断重复上述步骤，得到一个越来越接近根号三的值，但是我们永远无法得到一个精确的值。这是因为根号三是一个无理数。因此，我们只能使用无限循环的小数来接近这个数值。

在实际应用中，我们通常会将根号三或其他无理数表示为简化后的分数或小数形式。这样做会使得计算更加方便和准确。此外，在许多学科领域中，如物理学和工程学，我们经常需要精确计算根号三及其他无理数的值，而且通常使用专业软件和算法来实现。

总之，根号三是一个无理数，它可以用无限循环的小数来接近。我们可以使用长除法来计算根号三的值，但永远无法得到一个精确的值。在实际应用中，我们通常会将根号三表示为简化后的分数或小数形式，以方便计算和使用。

根号2约等于1414，根号3约等于1732，根号5约等于2232，根号7约等于2646。

根式乘除法法则：

1、同次根式相乘（除），把根式前面的系数相乘（除），作为积（商）的系数；把被开方数相乘（除），作为被开方数，根指数不变，然后再化成最简根式。

2、非同次根式相乘（除），应先化成同次根式后，再按同次根式相乘（除）的法则进行运算。

根式的加减法法则：各个根式相加减，应先把根式化成最简根式，然后合并同类根式。二次根式加减法法则：先把各个二次根式化简成最简二次根式，再把同类二次根式分别合并。

在根式的加减法中，同类根式要合并。一般地，几个根式总可以化成同次根式，但不一定能化成同类根式。

平方根和算术平方根的区别：

1、定义不同：如果x2=a，那么x叫做a的平方根。一个正数有两平方根，它们互为相反数；有一个平方根，它是0本身；负数没有平方根；如果x2=a，并且x≥0，那么x叫做a的算术平方根，一个正数的算术平方根只有一个，非负数的算术平方根一定是非负数。

2、表示方法不同：正数a的平方根，表示为±√a；正数a的算术平方根为√a。

1、演示使用的办公软件为office word，本次演示使用版本为Microsoft office家庭和学生版2016。

2、首先打开word办公文档，新建一张空白文档。

3、在最上方菜单栏中找到插入菜单，点击插入菜单后，在弹出的工具栏中找到符号下的公式按钮。

4、点击公式按钮之后我们会来到公式设计界面，在这里我们在工具栏中找到根式，然后点击插入自己想要输入的根号类型。

5、演示插入了一个最基本的根式符号，并进行了根号3的输入，实际使用请根据具体情况自行输入。

让我们逐步计算这个表达式：

1 首先，我们将2又1/4和-3又3/8相加。为了方便计算，我们可以转化为分数形式。2又1/4可以写成9/4，-3又3/8可以写成-27/8。然后，我们将这两个分数相加：

(9/4) + (-27/8) = (18/8) + (-27/8) = -9/8

2 接下来，我们对-9/8进行根号运算，然后再平方，其中根号平方即是对这个数开根号，然后再平方，等于去掉根号，只保留根号内的数。根号-9/8可以写成根号-9/根号8。注意到根号8等于根号(42)，可以分解为2根号2，所以根号8可以写成2根号2。因此，根号-9/8可以写成根号(-9)/(2根号2)。由于负数的平方根是虚数，我们表示根号(-9)为i根号9，即i√9。将这个代入，我们得到：

(i√9) / (2√2)

3 接下来，我们再对这个表达式进行简化。根号9等于3，所以i√9可以写成3i。将这个代入，我们有：

(3i) / (2√2)

4 最后，我们将这个表达式与-3相加，即-3 + (3i) / (2√2)。由于分母中有根号2，我们可以将分子分母同时乘以根号2，以消去根号2：

(-3√2 + 3i) / 2

综上所述，2又1/4加-3又3/8的根号平方3—l3—+兀I的计算结果为 (-3√2 + 3i) / 2。