(1+2)什么意思

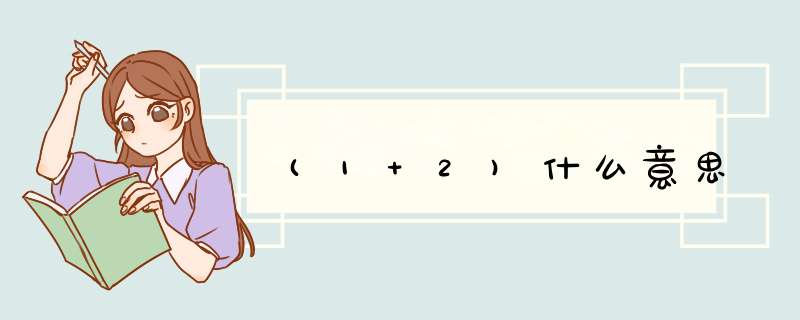
这是数学加法运算：1+2=3。

这里的加法运算在括号内，具有优先计算的权利，比如(1+2)×3，虽然有乘法，但是括号的优先级高于乘法，先计算括号内在计算括号外。

加法（通常用加号“+”表示）是算术的四个基本操作之一，其余的是减法，乘法和除法。 例如，在下面的中，共有三个苹果和两个苹果的组合，共计五个苹果。 该观察结果等同于数学表达式“3 + 2 = 5”，即“3加2等于5”。

扩展资料：

加法用术语之间的加号“+”编写；结果用等号表示。 例如，

还有一些情况，即使没有符号出现，

一个数字紧随其后的一个分数表示混合数。例如，

这个符号可能会引起争议，因为在大多数其他语境中，两个数字放在一起表示乘法。

一系列相关数字的总和可以通过σ符号表示，表示迭代。 例如，

数学家笛卡尔提出的浪漫极坐标曲线是什么曲线如下：

著名的数学家笛卡尔曾研究过花瓣和叶形的曲线，发现了现代数学中有名的“笛卡尔曲线”。辐射对称的花及螺旋排列的果，它们在数学上则符合黄金分割的规律。小麦的分蘖，是围绕着圆柱形的茎按黄金分割进行排列和展开的。常见的三叶草和常春藤的叶片形状，也可以用三角函数方程来表示。

以叶子为例，叶子的排列是建立在能充分获得光合作用面积和采集更多阳光这一基础上的。如车前草，有着轮生排列的叶片，叶片与叶片之间的夹角为137°30′，这是圆的黄金分割的比例。

梨树也是如此，它的叶片排列是沿对数螺旋上升，这也保证了叶与叶之间不会重合，下面的叶片正好在从上面叶片间漏下阳光的空隙地方，这是采光面积最大的排列方式。可见，沿对数螺旋按圆的黄金分割盘旋而生，是叶片排列的最优良选择。

高等植物的茎也有最佳的形态。许多草本植物的茎，它们的机械组织的厚度接近于茎直径的七分之一，这种圆柱形结构很符合工程上以耗费最少的材料而获得最大坚固性的一种形式。一些四棱形的茎，机械组织多分布于四角，这样也提高了茎的支撑能力，支持了较大的叶面积。

很久以前，数学家利用各种算法包括几何算法和分析算法来计算π值，非常费力，耗费时间长，计算效率低。如今，计算机诞生，计算速度超快，很快能计算出小数点后千万甚至上亿位，效率大大提高，显然升到更高境界。

圆周率π在数学中十分常见，常被应用于各种方面，如此重要不容忽视的数值当然少不了数学家的热切关注和产生的极大兴趣。鲁道夫·范·科伊是德国内一位著名的数学家，他将自己的后半生奉献给了数学研究，在十多年的时间内运用几何算法，成功精确计算出小数点后三十五位。显然，相比如今的计算技术，他的研究是低效率、高输入低输出的，但也激励了后人奋起研究圆周率，积极寻找计算方法。之后，有人成功研究出了另一种较之有效的方法，那就是分析方法，这也提高了计算圆周率π值的效率。当时印度的一位优秀数学家，名为拉马努金发现了两个公式，他充分利用这两个公式，很快就能手算出小数点后一百多位数，与鲁道夫利用的方法相比，其计算效率可不只是提高了百倍。

现在计算机出现了，数学家充分利用计算机，在计算机上不断推理演算，计算机超快的计算速度显然是数学家最看重的。他们将自己推理出来的公式输入计算机，进行无数次的模拟运算，望找到最为简便的计算公式。功夫不负有心人，梅钦公式和高斯-勒让德迭代算法被研究出来，计算机中被植入这些公式，人们使用圆周率更为普及。

这两种方法都能精准计算出圆周率，同时各有特色。梅钦公式就是一个公式，高斯-勒让德迭代算法中先给予初始值，然后反复迭代，使数值更加精准。

数学在发展，未知等待探索，我们仍需努力。