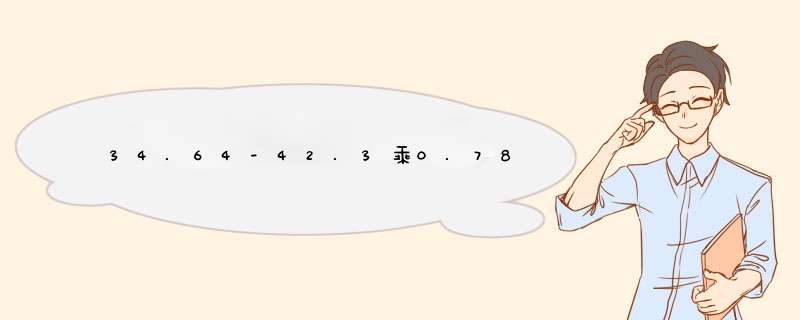
脱式计算,3464-423×078。
解题思路:在做这种脱式运算的时候,应该要先考虑括号里面的计算。然后再考虑先乘除计算,再进行加减运算。那么我们再具体运算的时候,就应该考虑上面的这些运算步骤,一步一步计算得到答案。这里可以先计算乘法运算,接着进行减法运算,得到答案。
详细的计算过程如下
3464-423×078
=3464-32994
=1646
所以,可以通过上面的脱式计算过程得到答案是1646。
扩展资料:
423×078=32994
第一步:008×423=3384
第二步:07×423=2961
第三步:累加上面两步计算答案,得到32994
所以,可以通过竖式计算的乘法运算,得到答案是32994。
分解因式的本质就是乘法运算的逆运算,因式也是经过乘法运算后的式子。
把一个多项式在一个范围(如有理数范围内分解,即所有项均为有理数)化为几个最简整式的积的形式,这种变形叫做因式分解,也叫作分解因式。
因式分解的方法有十字相乘法,待定系数法,双十字相乘法,对称多项式,轮换对称多项式法,余式定理法,提公因式法、运用公式法、分组分解法,拆项和添减项法式法,换元法,长除法,短除法,除法等。
1、a2-b2=(a+b)(a-b)
2、a2+2ab+b2=(a+b)2
3、a2-2ab+b2=(a-b)2
4、a3+b3=(a+b)(a2-ab+b2)
5、a3-b3=(a-b)(a2+ab+b2)
6、a3+3a2b+3ab2+b3=(a+b)3
7、a3-3a2b+3ab2-b3=(a-b)3
8、a2+b2+c2+2ab+2bc+2ca=(a+b+c)2
扩展资料:
完全平方公式
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍即完全平方公式。
与
都叫做完全平方公式.为了区别,我们把前者叫做两数和的完全平方公式,后者叫做两数差的完全平方公式。
这两个公式的结构特征是:左边是两个相同的二项式相乘,右边是三项式,是左边二中两项的平方和,加上(这两项相加时)或减去(这两项相减时)这两项乘积的2倍;公式中的字母可以表示具体的数(正数或负数),也可以表示单项式或多项式等代数式。
平方差公式:当乘式是两个数之和以及这两个数之差相乘时,积是二项式.这是因为具备这样特点的两个二项式相乘,积的四项中,会出现互为相反数的两项,合并这两项的结果为零,于是就剩下两项了.而它们的积等于乘式中这两个数的平方差,即
例:完全平方差
平方差
参考资料:
交叉相乘,是一种数学计算方法。
例如:a/c=b/d交叉相乘后得:ad=bc其实就是去分母,两端同时乘以cd。所以得出的ad=bc。
交叉相乘可以把四个数写成两个比,根据比值是否相等作出判断。也可将四个数分成两组,根据每组中两个数的乘积是否相等作出判断,其中运用比例的基本性质进行判断比较简便。
延伸十字相乘法:
十字左边相乘等于二次项,右边相乘等于常数项,交叉相乘再相加等于一次项。其实就是运用乘法公式运算来进行因式分解。
十字分解法能用于二次三项式(一元二次式)的分解因式(不一定是在整数范围内)。
对于像ax²+bx+c=(a1x+c1)(a2x+c2)这样的整式来说,这个方法的关键是把二次项系数a分解成两个因数a1,a2的积,把常数项c分解成两个因数c1,c2的积,并使a1c2+a2c1正好等于一次项的系数b。那么可以直接写成结果:ax²+bx+c=(a1x+c1)(a2x+c2)。
乘法也可以被视为计算排列在矩形(整数)中的对象或查找其边长度给定的矩形的区域。 矩形的区域不取决于首先测量哪一侧,这说明了交换属性。 两种测量的产物是一种新型的测量,例如,将矩形的两边的长度相乘给出其面积,这是尺寸分析的主题。
十字交叉相乘法分解因式就是通过乘法的运算公式去进行的因式分解。
1、因式分解:我们在学习一元二次方程的时候,最常用的一种方法其实就是因式分解了。因为因式分解的计算过程比较简单,我们只需要根据公式去计算出结果就好。因式分解有很多的方法,而十字交叉就是其中之一。
2、十字交叉法:十字相乘是解一元二次方程最简单的一个方法。因为我们只需要将式子分解成一种乘法公式的式子来直接求出结果。我们分解了之后,会形成一个新的式子,而我们的计算结果其实就已经是藏在了式子里面了。
3、一元二次方程:我们在学习一元二次方程的时候,会学习如何分解一元二次方程。一元二次方程的分解我们就会用到十字交叉,但是十字交叉的使用是分情况的。如果我们分解的时候,计算量比较大,并且还不一定可以出结果的时候,可以去试一试公式法。
所以,十字交叉法因式分解在很多时候确实是会给我们带来一个简便的计算,但不是所有的情况都适用。
x²+(a+b)x+ab=(x+a)(x+b)
十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数
具体步骤:
十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数
扩展资料:
原理:
运用了乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。
十字相乘法能把二次三项式分解因式(不一定在整数范围内)。
对于形如ax²+bx+c=(a1x+c1)(a2x+c2)的整式计算步骤:
⑴把二次项系数a分解成两个因数a1,a2的积a1·a2
⑵把常数项c分解成两个因数c1,c2的积c1·c2
⑶使a1c2+a2c1正好等于一次项的系数b
⑷结果:ax²+bx+c=(a1x+c1)(a2x+c2)
实质:二项式乘法的逆过程。
当首项系数不是1时,需注意各项系数的符号。基本式子:x²+(p+q)x+pq=(x+p)(x+q)。
1、y^2-2y-x^2+1
2、(3a+2b)^2-2(3a+2b)(2b-3a)+(3a-2b)^2
3、 -m^3n^3+4m^2n^2-mn
4、 (x+1)(x+3)(x+5)(x+7)+15
5、 x^2-2xy+y^2-13x+13y+30
6、 4(x+2z)(x-2z)+12xy+9y^2
7、 a^4+(a+b)^4+b^4
8、 6x^2-7xy-3y^2-x+7y-2
9、 x^2+x-2
10、x^2-4xy+3y^2-x-y-2
11、x^2+3x-(a^2+a-2)
12、(2x+y)^2-(x+2y)^2
13、(m+n)^2-n^2
14、169(a-b)^2-196(a-b)^2
15、(a+b+c)^2-(a-b-c)^2
16、4(2p+3q)^2-(3p-q)^2
17、3ax^2-3ay^4
18、8y^4-2y^2
19、a^2-10ab+25b^2-5a+25b-6
20、x^2+2xy+y^2-x-y+1/4
21、a^2-6ab+9b^2-4a+12b+4
22、x^3+2x^2-5x-6
23、x^2-xy-2y^2-x-y
24、05(m+1)^2+2(m+1)(1-m)+2(m-1)^2
25、4xy^2-4x^2y-y^3
26、(4a^2 +1)^2 -16a^2
27、5^2008-75^2007+10^2006+2008
28、a^4+b^4-2a^2b^2
29、x(a-x)(a-y)-y(x-a)(y-a)
因式分解的十二种方法 :
把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解。因式分解的方法多种多样,现总结如下:
1、 提公因法
如果一个多项式的各项都含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。
例1、 分解因式x -2x -x(2003淮安市中考题)
x -2x -x=x(x -2x-1)
2、 应用公式法
由于分解因式与整式乘法有着互逆的关系,如果把乘法公式反过来,那么就可以用来把某些多项式分解因式。
例2、分解因式a +4ab+4b (2003南通市中考题)
解:a +4ab+4b =(a+2b)
3、 分组分解法
要把多项式am+an+bm+bn分解因式,可以先把它前两项分成一组,并提出公因式a,把它后两项分成一组,并提出公因式b,从而得到a(m+n)+b(m+n),又可以提出公因式m+n,从而得到(a+b)(m+n)
例3、分解因式m +5n-mn-5m
解:m +5n-mn-5m= m -5m -mn+5n
= (m -5m )+(-mn+5n)
=m(m-5)-n(m-5)
=(m-5)(m-n)
4、 十字相乘法
对于mx +px+q形式的多项式,如果a×b=m,c×d=q且ac+bd=p,则多项式可因式分解为(ax+d)(bx+c)
例4、分解因式7x -19x-6
分析: 1 -3
7 2
2-21=-19
解:7x -19x-6=(7x+2)(x-3)
5、配方法
对于那些不能利用公式法的多项式,有的可以利用将其配成一个完全平方式,然后再利用平方差公式,就能将其因式分解。
例5、分解因式x +3x-40
解x +3x-40=x +3x+( ) -( ) -40
=(x+ ) -( )
=(x+ + )(x+ - )
=(x+8)(x-5)
6、拆、添项法
可以把多项式拆成若干部分,再用进行因式分解。
例6、分解因式bc(b+c)+ca(c-a)-ab(a+b)
解:bc(b+c)+ca(c-a)-ab(a+b)=bc(c-a+a+b)+ca(c-a)-ab(a+b)
=bc(c-a)+ca(c-a)+bc(a+b)-ab(a+b) =c(c-a)(b+a)+b(a+b)(c-a) =(c+b)(c-a)(a+b)
7、 换元法
有时在分解因式时,可以选择多项式中的相同的部分换成另一个未知数,然后进行因式分解,最后再转换回来。
例7、分解因式2x -x -6x -x+2
解:2x -x -6x -x+2=2(x +1)-x(x +1)-6x
=x [2(x + )-(x+ )-6
令y=x+ , x [2(x + )-(x+ )-6
= x [2(y -2)-y-6]
= x (2y -y-10)
=x (y+2)(2y-5)
=x (x+ +2)(2x+ -5)
= (x +2x+1) (2x -5x+2)
=(x+1) (2x-1)(x-2)
8、 求根法
令多项式f(x)=0,求出其根为x ,x ,x ,……x ,则多项式可因式分解为f(x)=(x-x )(x-x )(x-x )……(x-x )
例8、分解因式2x +7x -2x -13x+6
解:令f(x)=2x +7x -2x -13x+6=0
通过综合除法可知,f(x)=0根为 ,-3,-2,1
则2x +7x -2x -13x+6=(2x-1)(x+3)(x+2)(x-1)
9、 图象法
令y=f(x),做出函数y=f(x)的图象,找到函数图象与X轴的交点x ,x ,x ,……x ,则多项式可因式分解为f(x)= f(x)=(x-x )(x-x )(x-x )……(x-x )
例9、因式分解x +2x -5x-6
解:令y= x +2x -5x-6
作出其图象,见右图,与x轴交点为-3,-1,2
则x +2x -5x-6=(x+1)(x+3)(x-2)
10、 主元法
先选定一个字母为主元,然后把各项按这个字母次数从高到低排列,再进行因式分解。
例10、分解因式a (b-c)+b (c-a)+c (a-b)
分析:此题可选定a为主元,将其按次数从高到低排列
解:a (b-c)+b (c-a)+c (a-b)=a (b-c)-a(b -c )+(b c-c b)
=(b-c) [a -a(b+c)+bc]
=(b-c)(a-b)(a-c)
11、 利用特殊值法
将2或10代入x,求出数P,将数P分解质因数,将质因数适当的组合,并将组合后的每一个因数写成2或10的和与差的形式,将2或10还原成x,即得因式分解式。
例11、分解因式x +9x +23x+15
解:令x=2,则x +9x +23x+15=8+36+46+15=105
将105分解成3个质因数的积,即105=3×5×7
注意到多项式中最高项的系数为1,而3、5、7分别为x+1,x+3,x+5,在x=2时的值
则x +9x +23x+15=(x+1)(x+3)(x+5)
12、待定系数法
首先判断出分解因式的形式,然后设出相应整式的字母系数,求出字母系数,从而把多项式因式分解。
例12、分解因式x -x -5x -6x-4
分析:易知这个多项式没有一次因式,因而只能分解为两个二次因式。
解:设x -x -5x -6x-4=(x +ax+b)(x +cx+d)
= x +(a+c)x +(ac+b+d)x +(ad+bc)x+bd
所以 解得
则x -x -5x -6x-4 =(x +x+1)(x -2x-4)
欢迎分享,转载请注明来源:浪漫分享网

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)